BEHIND THE PAPER
Moving away from alchemy into the age of science for deep learning
by Andrzej Banburski
Imagine you’re back in elementary school and just took your first statistics course on fitting models to data. One thing you’re sure about is that a good model surely should have less parameters than data (think of fitting ten data points with a line, i.e. two parameters), otherwise you’ll ruin the predictivity of your model by overfitting. But then deep learning shows up, where the best practice seems to be perfectly fitting your training data with many more parameters – so many in fact that you can fit random noise with your model (think of fitting ten data points with a polynomial of a thousand coefficients). How can this be? Do we need to completely rethink the basics of statistical learning theory?
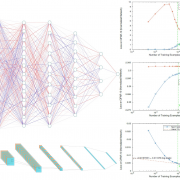
This is a question we set out to answer in our new Nature Communications paper. Our suspicions were that no magic would be necessary to understand deep nonlinear neural networks, and so we turned our attention first to understanding how exactly the classic case of linear problems works. It has been known for some time that in linear systems that have more unknowns than equations there are infinitely many solutions. However, if we try solving this system by the technique of gradient descent (which is what we also use to train deep nets), while imposing a constraint that the “size”, or norm, of our parameters doesn’t grow too big, we find a solution known as the Moore-Penrose pseudo-inverse. This turns out in practice to work remarkably well - in fact it’s the best known solution in linear regression that does well on unseen data. The problem we faced however is that deep networks work well even without imposing any such constraints!
A small, entirely skippable, technical aside for the curious reader: whether our machine learning model will overfit to the training data actually depends on how “complex” the class of models is. This complexity can be measured in multiple ways, many of them less naive than just straightforward parameter counting, with some of the more often used being Vapnik–Chervonenkis (VC) dimension, covering numbers, or Rademacher complexity. What is important to understand about these measures of complexity is that they do depend on the size of the parameters of the model, and hence a constraint on this norm should imply less overfitting. The question then is “where is this hidden complexity control?”...
Read the full blog entry on Nature.com's website using the link below.