Introduction
The central nervous system transforms external stimuli into neural representations (hereafter “reps” for brevity), which form the basis for behavior learning and action selection [1]. Progress in neurophysiology, especially in the last decade, has begun to reveal aspects of the neural reps employed by humans and other animals
[2–5]. Parallel progress in machine learning has produced numerical methods for automatically learning neural reps, used by artificial systems, that successfully inform behavior learning [6–8] and action selection [6–9]. In some cases, neural reps discovered numerically even resemble those observed in animals [9,10]. Ironically, however, due to the automatic nature of machine learning methods, it is usually difficult to extract general lessons and intuition from case applications. The situation is such that principles generalizing across domains are both rare and desirable.
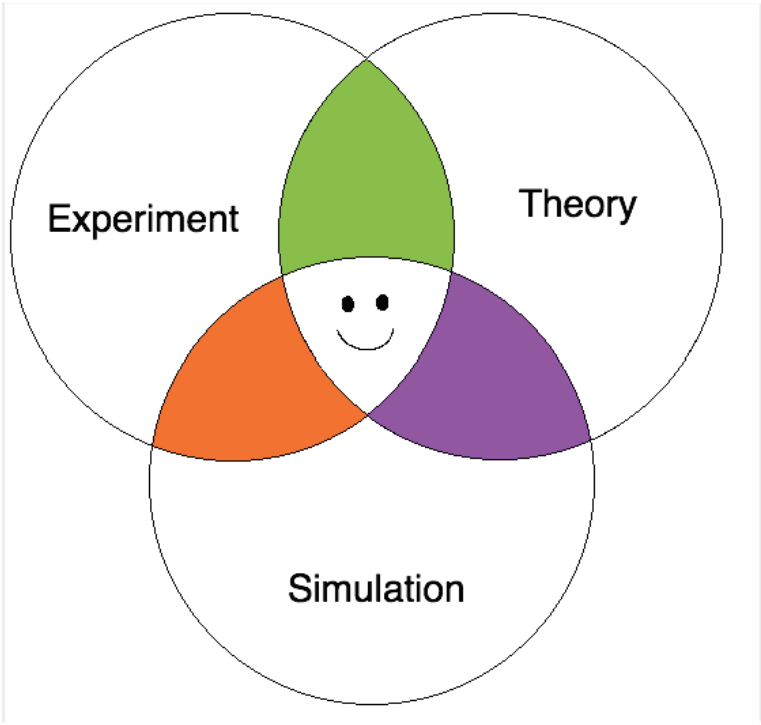
Figure 1. We are excited about exploring the interfaces.
We are excited about a number of approaches to studying neural reps that focus on the interfaces between theory, experiment and simulation as illustrated by the Venn diagram in Figure 1. These approaches fall within the CBMM thrust “Circuits of Intelligence” and also connect with the thrust “Theoretical Frameworks for Visual Intelligence”. MIT postdoc Luís Seoane and graduate student David Theurel are both very excited to work on this project, and we welcome additional participants.
Theory-Experiment link
At the interface between theory and experiment, we are interested in using the representation theory of Lie groups, a powerful branch of mathematics, to study how transformations of the external world might be represented in the brain. We feel that this line of research may provide a principled, unified way to understand the computational lives of various types of neurons. Our early work in this direction has focused on neurons coding for space, time and motion; our preliminary results suggest it is possible, under certain technical assumptions, to calculate the effect of a mouse’s locomotion on the activity of its hippocampal place cells, grid cells, head direction cells, speed cells, and others. (See [2–5] for descriptions of these neuron types.) As a concrete example, Figure 2 shows our preliminary prediction for the firing phase and firing rate of a place cell as functions of a mouse’s position and running speed. (See [11] for a description of rate coding and phase coding in place cells.) Models obtained from our framework can be tested against data in the literature , and may suggest interesting directions for future experiments.
Also at the interface between theory and experiment, in the past few years there have been several theoretical studies motivated by the beautiful geometrical pattern of grid cell firing fields [12–14]. The central lesson to emerge from this research is that, computationally, grid cells represent the optimal way to code for position, at a prescribed spatial resolution, while minimizing the total number of neurons involved. Inspired by this success story, we ask whether place cells can likewise be characterized as coding for position while minimizing the use of some resource. Our working hypothesis is that they may be the answer the question of how to code for position, at a prescribed resolution, while minimizing the number of neurons active at any one time given appropriate constraints.
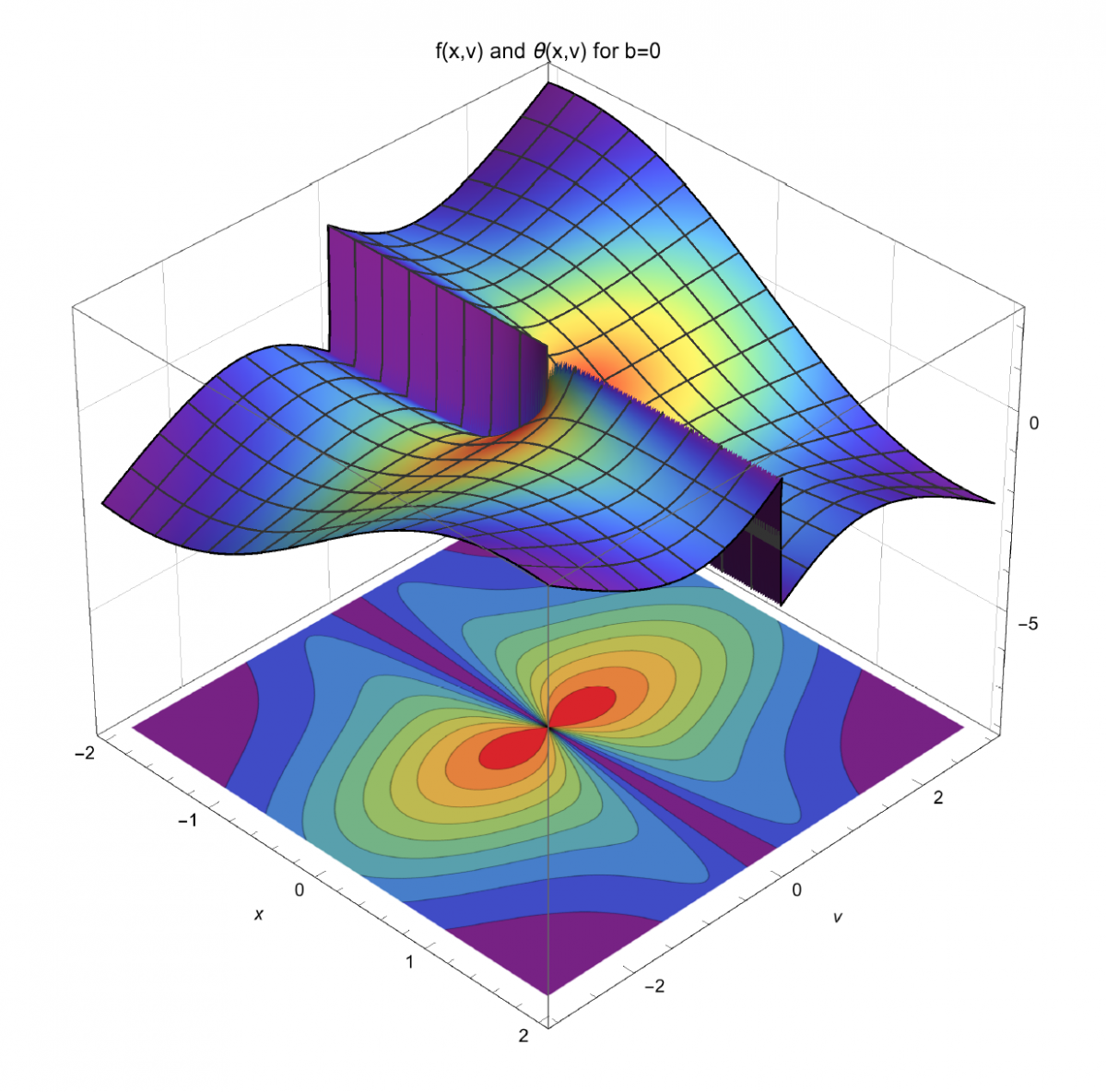
Figure 2. Firing phase (top, 3D surface) and firing rate (bottom, 2D contour plot, also projected onto 3D surface) of a place cell, as function of distance, x, traveled through place field, and running speed, v, for rectilinear motion passing through the field peak. Theoretical calculation relying on rep theory. Units omitted.
Simulation-Experiment link
Also at the interface between theory and experiment, in the past few years there have been several theoretical studies motivated by the beautiful geometrical pattern of grid cell firing fields [12–14]. The central lesson to emerge from this research is that, computationally, grid cells represent the optimal way to code for position, at a prescribed spatial resolution, while minimizing the total number of neurons involved. Inspired by this success story, we ask whether place cells can likewise be characterized as coding for position while minimizing the use of some resource. Our working hypothesis is that they may be the answer the question of how to code for position, at a prescribed resolution, while minimizing the number of neurons active at any one time given appropriate constraints.
At the interface between experiment and simulation, we ask whether these coding schemes employed by grid cells and place cells coincide with any simple schemes invented by humans, and in particular, whether they are the solution to a biologically motivated optimization problem that can be efficiently simulated on a computer. Our early work indicates that grid cells use a coding scheme related to Principal Component Analysis (PCA), while place cells use a scheme related to Independent Component Analysis (ICA), as illustrated in figure 3. We aim to explore whether both grid cells and place cells can be rigorously obtained as the solution to different optimization problems, extending the work of e.g. [15,16]. For example, maximization of noisy autoencoder accuracy almost gives grid cells, but some elusive ingredient is still missing from the minimization problem to yield grid cells like those experimentally observed.
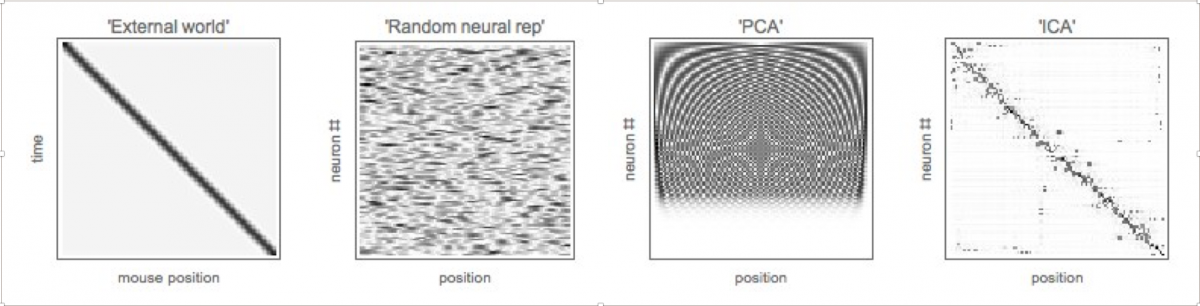
Figure 3. A hypothetical mouse moves along a linear track. We show the space-time diagram of its motion (far left), a random neural representation of this motion (left), the PCA representation (right), and the ICA representation (far right). “PCA neurons” exhibit periodic firing fields, while “ICA neurons” exhibit firing fields that are localized in space.
If we succeed in reproducing experimentally observed grid cells, place cells and other neural representations by running biologically motivated simulation/optimization, then this offers the opportunity to test the above-mentioned Lie-group based theoretical predictions directly on the simulations, even for experiments that have not yet been carried out in the laboratory. For example, the unitary rep theory makes predictions not only for how a mouse represents its position and orientation, but also for how it represents its location in the full phase space (position, orientation, velocity and angular velocity). If these theory-simulation comparisons are successful, it will motivate performing specific laboratory experiments where these same predictions can be experimentally tested — indeed, experiments that CBMM PI’s are in a perfect position to perform.
Finally, symbolized by the smily face in Fig. 1, we hope that the interplay between our models and our algorithms will help improve our theory, our simulations, and our understanding of the neural representation of space, time and motion.
References
[1] Decharms, R. Christopher, and Anthony Zador. "Neural representation and the cortical code." Annual review of neuroscience 23.1 (2000): 613-647.
[2] Rowland, David C., et al. "10 Years of Grid Cells." Annual Review of Neuroscience 39.1 (2016).
[3] Finkelstein, Arseny, Liora Las, and Nachum Ulanovsky. "3D Maps and Compasses in the Brain." Annual Review of Neuroscience 39.1 (2016).
[4] Kropff, Emilio, et al. "Speed cells in the medial entorhinal cortex." Nature (2015).
[5] Lusk, Nicholas A., et al. "Cerebellar, hippocampal, and striatal time cells." Current Opinion in Behavioral Sciences 8 (2016): 186-192.
[6] Sutton, Richard S., and Andrew G. Barto. Reinforcement learning: An introduction. MIT press, 1998.
[7] Mnih, Volodymyr, et al. "Human-level control through deep reinforcement learning." Nature 518.7540 (2015): 529-533.
[8] Silver, David, et al. "Mastering the game of Go with deep neural networks and tree search." Nature 529.7587 (2016): 484-489.
[9] Krizhevsky, Alex, Ilya Sutskever, and Geoffrey E. Hinton. "Imagenet classification with deep convolutional neural networks." Advances in neural information processing systems. 2012.
[10] Bell, Anthony J., and Terrence J. Sejnowski. "The “independent components” of natural scenes are edge filters."
Vision research 37.23 (1997): 3327-3338.
[11] O'Keefe, John, and Neil Burgess. "Dual phase and rate coding in hippocampal place cells: theoretical significance and relationship to entorhinal grid cells." Hippocampus 15.7 (2005): 853-866.
[12] Mathis, Alexander, Andreas VM Herz, and Martin B. Stemmler. "Resolution of nested neuronal representations can be exponential in the number of neurons." Physical review letters 109.1 (2012): 018103.
[13] Mathis, Alexander, Andreas VM Herz, and Martin B. Stemmler. "Multiscale codes in the nervous system: the problem of noise correlations and the ambiguity of periodic scales." Physical Review E 88.2 (2013): 022713.
[14] Wei, Xue-Xin, Jason Prentice, and Vijay Balasubramanian. "The sense of place: grid cells in the brain and the transcendental number e." arXiv preprint arXiv:1304.0031 (2013).
[15] Kropff, Emilio & Treves, Alessandro (2016), “The Emergence of Grid Cells: Intelligent Design or Just A!daptation?”, Hippocampus, 18:1256–1269 (2008)
[16] Si, Bailu & Kropff , Emilio, “Grid alignment in entorhinal cortex”, Biol Cybern (2012) 106:483–506