- Motivation
- Temporal Shifting Overview
- Defining the Temporal Dimension
- Defining Models
- Running Models
Motivation
Consider feedforward models that deal with temporal data, such as video. There are two cases to consider:
- (Simple) All operations occur within a single frame of time. Implementation of such a model is easy. All you need is an outer loop in MATLAB that loads the next single frame into the GPU, calls cns('run') to process it, and then retrieves the result. The CNS model itself does not need to store multiple frames or even "know" about time.
- (Harder) The model contains at least some layers that combine information from multiple frames. Example operations could include temporal smoothing or computing responses to spatiotemporal features. One could loosely label all such operations as performing "convolution over time".
CNS's temporal shifting feature is designed for this latter case. It is best appreciated by first discussing what we would have to do without it.
In principle, one could treat time just like any other dimension over which convolution is performed. The problem with this is: the time dimension is often very large. An entire video may not fit into GPU memory. Video data typically needs to be handled in a streaming manner.
A seemingly simple way to do streaming would be: define a CNS model that will hold a fixed, manageable number of frames in GPU memory, then write outer-loop MATLAB code to break the video into blocks of frames and push the blocks through CNS one block at a time. However, this turns out to be nontrivial when you get into the details.
- For every layer, for every frame that is computed, you would have to ensure that all the frames it depends on in "lower" layers were still in GPU memory.
- Layers don't always have the same temporal resolution. For example, a model layer might do temporal smoothing and downsampling (from say 30 frames/sec down to 15 frames/sec).
- Temporal receptive fields are typically overlapping, so your blocks of input frames would also need to overlap. In other words, at least some input frames would end up being loaded more than once.
- You will generally want to load as many input frames in one block as your model complexity and GPU memory will allow, as this maximizes the potential for parallel processing to occur.
All this makes the problem of deciding where to "cut" the video into blocks rather tricky, and because you'll probably want to optimize for throughput, you won't want to do the calculations by hand, either.
CNS's temporal shift feature takes care of all these problems for you.
Temporal Shifting Overview
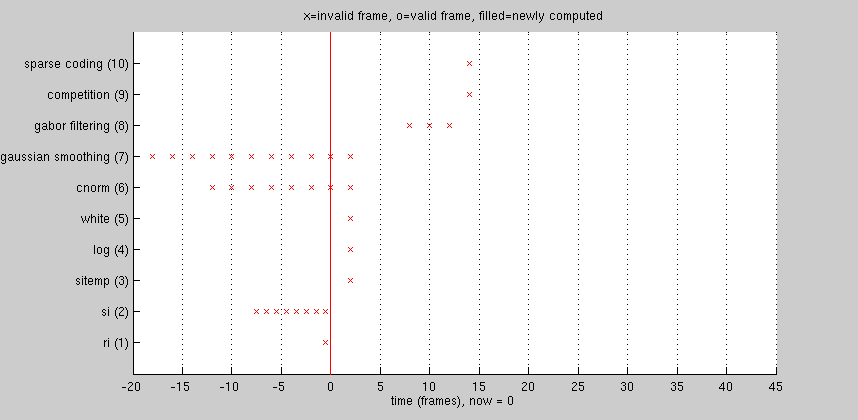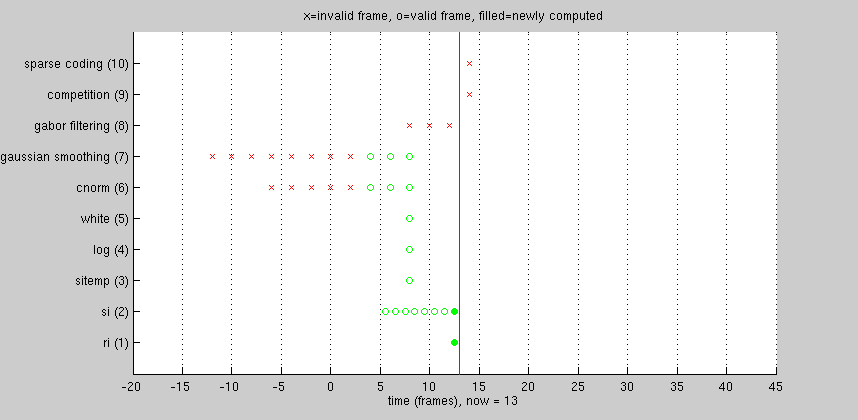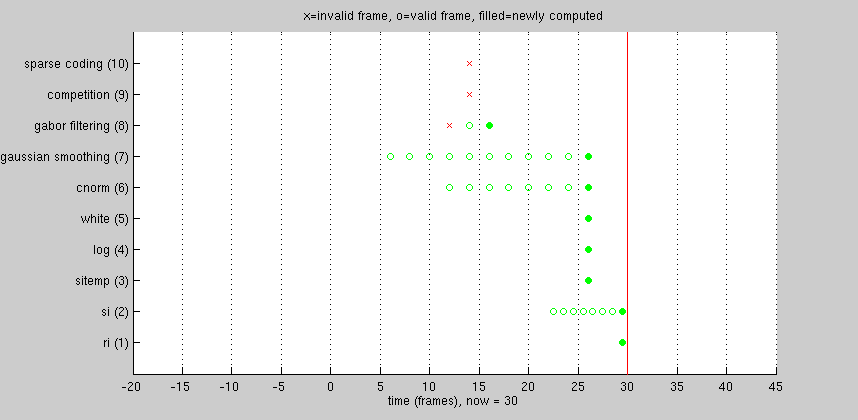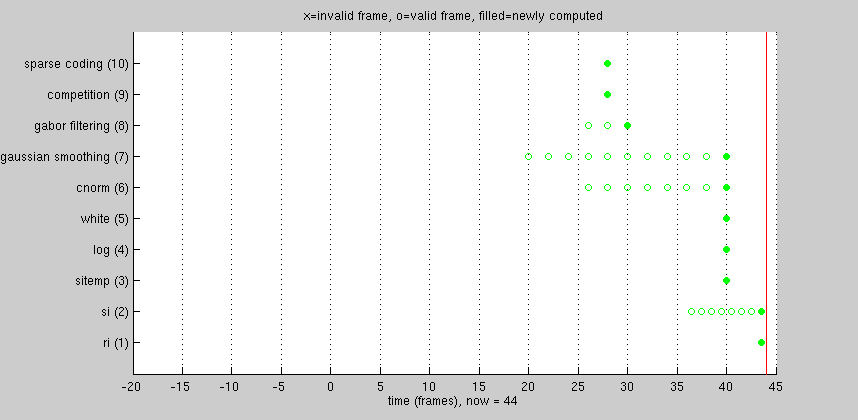
The animation below illustrates a CNS model that uses temporal shifting. There are 10 layers in total, going from bottom to top. Only the time dimension of each layer is shown. Each layer's time dimension is mapped to a common coordinate system, shown increasing from left to right. An "x" or "o" marks the center of each frame's receptive field in time.
Time is measured in "units": by definition, input frames are one unit apart. Before processing starts, the current time is zero, and all frames of all layers are marked "invalid" -- no input frames have been loaded, and nothing has been computed yet.
As time advances, the number of frames in each layer remains the same, but frames representing the oldest times are dropped, and new frames are loaded (or computed) for newer times. Consider layer 6, having eight frames numbered 1-8. At time now=28, frame index #8 contains a newly-computed frame centered at t=24.
Current time: Layer 6: temporal center of frame index #1: #2: #3: #4: #5: #6: #7: #8: now=28 10 12 14 16 18 20 22 24 now=30 12 14 16 18 20 22 24 26 now=32 14 16 18 20 22 24 26 28 now=34 16 18 20 22 24 26 28 30 now=36 18 20 22 24 26 28 30 32 now=38 20 22 24 26 28 30 32 34 now=40 22 24 26 28 30 32 34 36 now=42 24 26 28 30 32 34 36 38 now=44 26 28 30 32 34 36 38 40
As time advances further, the frame centered at t=24 gets shifted to the left within the layer, into progressively smaller indices, finally winding up in frame index #1 at time now=42. Two time steps later, the frame has been dropped entirely.
Now consider the model as a whole. Note that for different layers, the most recent frame is often centered at a different time. Higher layers tend to lag behind lower ones. This occurs for two reasons.
- Higher layers sometimes downsample in time. In this model, layer 3 computes one frame every two units of time, so all layers from 3 upwards have half the temporal resolution of the input. Thus, half the time, loading a single input frame doesn't change layers 3 and above at all.
- CNS's common coordinate system is based on receptive field centers, and the animation shows the center of each frame's temporal receptive field. Frames in higher layers that perform convolution over time are temporally centered in the middle of the temporal span of their input frames in lower layers.
In the illustrated model, layer 10 is considered the output layer. Only after 32 frames of input have been processed does the first output frame becomes available. After that, a new output frame is available every two input frames.
A given input frame never needs to be loaded twice.
Loading multiple frames. In the above animation, only a single frame is loaded at a time. In practice, one specifies the maximum number of frames one wishes to load at once, and CNS will automatically determine the required size of every layer such that the above-mentioned constraints are all satisfied. Loading many input frames at once can generate many output frames at once.
Defining the Temporal Dimension
Temporal shifting is activated by first identifying the temporal dimension for your cell types. As with other mapped dimensions, this is done via the dmap property. For the temporal dimension, set dmap = 2. For example:
p.dnames = {'f' 't' 'y' 'x'};
p.dims = {1 2 1 2};
p.dparts = {2 2 1 1};
p.dmap = [0 2 1 1];
Note:
- There can be at most one temporal dimension.
- If it exists, it must have dims = 2 and have the highest value of dparts for internal dimension 2.
- It doesn't have to be named 't', but naming it anything else seems like a bad idea to me.
Defining Models
For each layer in your model that has a temporal dimension, you need to establish the temporal mapping, i.e., where each frame is initially centered in time (as illustrated above). This is done in a manner similar to that for other mapped dimensions, using the cns_mapdim function.
cns_mapdim has two modes designed specifically for temporal mapping:
| Mode | Usage |
| 'temp1' | Used for input layers, i.e., layers you are going to load data into, not ones that get computed.
Syntax:
Additional arguments:
|
| 'temp2' | Used for layers that compute their results from other layers, i.e., probably most of the layers in any model.
Syntax:
Additional arguments:
Together, pzs(1), rfSizes(1), and rfStep determine the temporal mapping of layer z. cns_mapdim checks any additional elements pzs(2:end) and rfSizes(2:end) to ensure that those layers will always retain enough frames in memory to compute frames in layer z. |
Running Models
The following example script shows how to process frames through a model that employs temporal shifting. Assume we are dealing with 4-D layers, as above, with time as the second dimension, and assume that every cell type has a 'val' field that is either loaded as input or computed.
New cns commands/options, specific to temporal shifting, are shown in red and described after the example script.
The new cns commands (or new options for existing commands) used for temporal shifting are as follows.
| Command | Description |
| 'shift' | This is a new command which shifts all layers forward along their time dimension, dropping old frames and freeing space for new ones, as illustrated above.
Syntax:
Arguments:
Performance note: the shift command does not actually move the contents of GPU memory. An efficient circular buffer technique, transparent to the CNS programmer, is employed. |
| 'run' 'step' |
The syntax for the cns('run') and cns('step') commands is unchanged, but when there is a temporal dimension, only the new frames for each layer are computed.
Note that this means if you call cns('run') or cns('step') without first calling cns('shift'), nothing will be done. |
| 'get' 'set' |
The cns('get') and cns('set') commands have only one new option relating to temporal shifting: the special index 0 for the temporal dimension means "all new frames". For example, if a layer has 8 frames, and the most recent cns('shift') caused it to shift by 3 frames, then asking for temporal index 0 for this layer is the same as asking for temporal indices 6:8. |